Introducción a límites

Google Classroom

Microsoft Teams

Los límites describen cómo se comporta una función cerca de un punto, en vez de en ese punto. Esta simple pero poderosa idea es la base de todo el cálculo.

Para entender qué son los límites, consideremos un ejemplo. Empezamos con la función $\mathrm{}$.

$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$$$$$$

Se grafica la función f. El eje x va de 0 a 9. La gráfica consta de una recta que empieza en (0, 2), se mueve hacia arriba, pasa a través de (2, 4) y (4, 6) y termina en (7,9).web+graphie://cdn.kastatic.org/ka-perseus-graphie/507e8f38d9db338d657f07b535ba2ed4a8a9d206

El límite de $$ en $\mathrm{}$ es el valor al cual se aproxima $$ a medida que nos acercamos más y más a $\mathrm{}$. Gráficamente, es el valor de $$ al que tendemos en la gráfica de $$ al acercarnos más y más al punto de la gráfica donde $\mathrm{}$.

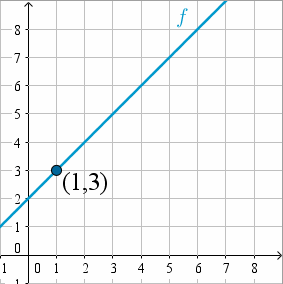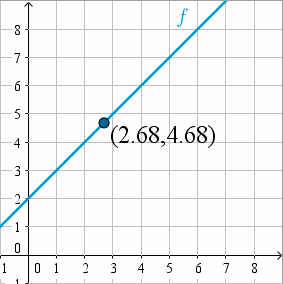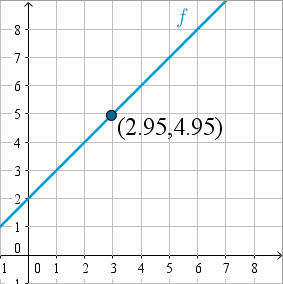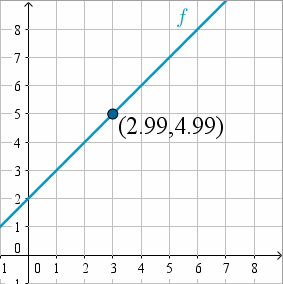
Por ejemplo, si partimos del punto $\mathrm{}\mathrm{}$ y nos movemos en la gráfica hasta estar muy cerca de $\mathrm{}$, entonces nuestro valor $$ (es decir, el valor de la función) está muy cerca de $\mathrm{}$.

La gráfica de la función f está animada. Un punto se mueve hacia arriba sobre la recta desde (1, 3) hasta (2.99, 4.99).

Creado con Geogebra.

Similarmente, si empezamos en $\mathrm{}\mathrm{}$ y nos movemos a la izquierda hasta estar muy cerca de $\mathrm{}$, el valor $$ nuevamente estará muy cerca de $\mathrm{}$.

La gráfica de la función f está animada. Un punto se mueve hacia abajo sobre la recta desde (5, 7) hasta (3.01, 5.01).

Creado con Geogebra.

Por estas razones, decimos que el límite de $$ en $\mathrm{}$ es $\mathrm{}$.

$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$$$$$$

La gráfica de la función f tiene flechas que apuntan a lo largo de la recta, hacia arriba y a la derecha y hacia abajo y a la izquierda, respectivamente, en dirección del punto (3, 5).

Tal vez te preguntes cuál es la diferencia entre el límite de $$ en $\mathrm{}$ y el valor de $$ en $\mathrm{}$, es decir, $\mathrm{}$.

Y sí, el límite de $\mathrm{}$ en $\mathrm{}$ es igual a $\mathrm{}$, pero este no siempre es el caso. Para entender esto, consideremos la función $$. Esta función es igual a $$, excepto que no está definida para $\mathrm{}$.

$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$$$$$$

Se grafica la función g. El eje x va de 0 a 9. La gráfica consta de una recta que empieza en (0, 2), se mueve hacia arriba, pasa a través de (2, 4) y de un círculo abierto en (3, 5) y termina en (7, 9).

$$

$\begin{array}{ll}\mathrm{}& \mathrm{}\\ \\ & \mathrm{}\end{array}$

$$${\displaystyle \frac{{}^{\mathrm{}}\mathrm{}}{\mathrm{}}}$$\mathrm{}$$$

$\begin{array}{rl}& {\displaystyle \frac{{}^{\mathrm{}}\mathrm{}}{\mathrm{}}}\\ \\ & {\displaystyle \frac{\mathrm{}\cancel{\mathrm{}}}{\cancel{\mathrm{}}}}\\ \\ & \mathrm{}\mathrm{}\end{array}$

Tal como con $$, el límite de $$ en $\mathrm{}$ es $\mathrm{}$. Esto se debe a que aún podemos acercarnos mucho a $\mathrm{}$ y los valores de la función se acercarán muchísimo a $\mathrm{}$.

$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$$$$$$

La gráfica de la función g tiene flechas que apuntan a lo largo de la recta, hacia arriba y a la derecha y hacia abajo y a la izquierda, respectivamente, en dirección del círculo abierto en (3, 5).

Así que el límite de $$ en $\mathrm{}$ es igual a $\mathrm{}$, ¡pero el valor de $$ en $\mathrm{}$ no está definido! ¡No son lo mismo!

Esa es la belleza de los límites: no dependen del valor real de la función en el límite. Describen cómo se comporta la función al acercarse al límite.

PROBLEMA 1

Esta es la gráfica de $$.

$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$$$$$$

¿Cuál es una estimación razonable para el límite de $$ en $\mathrm{}$?

Escoge 1 respuesta:

Escoge 1 respuesta:

• (Elección A)   

  $\mathrm{}$
• (Elección B)   

  $\mathrm{}$
• (Elección C)   

  $\mathrm{}$
• (Elección D)   

  El límite no existe

Tenemos también una notación especial para hablar de límites. Así es como escribimos el límite de $$ cuando $$ se acerca (o tiende a) $\mathrm{}$:

$\begin{array}{rl}\phantom{}\phantom{}& \phantom{}\phantom{}\\ & \\ {\displaystyle \underset{\mathrm{}}{}}& \\ \\ \mathrm{}\end{array}$

El símbolo ${\displaystyle }$ significa que tomamos el límite de algo.

La expresión a la derecha de ${\displaystyle }$ es la expresión de la cual tomamos el límite. En nuestro caso, se trata de la función $$.

La expresión $\mathrm{}$ que aparece debajo de ${\displaystyle }$ significa que tomamos el límite de $$ a medida que los valores de $$ se acercan a $\mathrm{}$.

PROBLEMA 2

Esta es la gráfica de $$.

$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$$$$$$

¿Cuál es una estimación razonable para ${\displaystyle \underset{\mathrm{}}{}}$?

Escoge 1 respuesta:

Escoge 1 respuesta:

• (Elección A)   

  $\mathrm{}$
• (Elección B)   

  $\mathrm{}$
• (Elección C)   

  $\mathrm{}$
• (Elección D)   

  El límite no existe

PROBLEMA 3

¿Cuál expresión representa el límite de ${}^{\mathrm{}}$ cuando $$ tiende a $\mathrm{}$?

Escoge 1 respuesta:

Escoge 1 respuesta:

• (Elección A)   

  ${\displaystyle {\mathrm{}}^{\mathrm{}}}$
• (Elección B)   

  ${\displaystyle \underset{{}^{\mathrm{}}\mathrm{}}{}}$
• (Elección C)   

  ${\displaystyle \underset{\mathrm{}}{}{}^{\mathrm{}}}$
• (Elección D)   

  ${\displaystyle \underset{\mathrm{}}{}}$

En los límites, queremos estar infinitamente cerca.

¿Qué queremos decir con "infinitamente cerca"? Examinemos los valores de $\mathrm{}$ a medida que los valores de $$ se acercan mucho a $\mathrm{}$. (Recuerda que al hablar de límites no nos interesa $\mathrm{}$ en sí).

Podemos ver que cuando los valores de $$ son menores que $\mathrm{}$, pero se acercan más y más, los valores de $$ se acercan más y más a $\mathrm{}$.

También vemos que cuando los valores de $$ son mayores que $\mathrm{}$, pero se acercan más y más, los valores de $$ se acercan más y más a $\mathrm{}$.

Observa que con lo que más nos acercamos a $\mathrm{}$ es con $\mathrm{}\mathrm{}$ y $\mathrm{}\mathrm{}$, que están a $\mathrm{}$ unidades de distancia de $\mathrm{}$.

Podemos acercarnos más, si así lo deseamos. Por ejemplo, supongamos que queremos estar a $\mathrm{}$ unidades de $\mathrm{}$; entonces podemos escoger $\mathrm{}$ y en ese caso $\mathrm{}\mathrm{}$.

Esto no tiene fin. Siempre podemos acercarnos más a $\mathrm{}$. Pero ¡de eso se trata "infinitamente cerca"! Como "infinitamente cerca" no es posible en la realidad, lo que queremos decir con ${\displaystyle \underset{\mathrm{}}{}\mathrm{}}$ es que no importa cuánto queramos acercarnos a $\mathrm{}$, existe un valor de $$ muy cercano a $\mathrm{}$ que nos llevará ahí.

Si esto te parece difícil de captar, quizá esto te ayude: ¿cómo sabemos que hay un número infinito de números enteros diferentes? No es como si los contáramos todos y llegáramos a infinito. Sabemos que son infinitos porque para cada número entero hay uno que es aún mayor que ese. Siempre hay otro, y otro más.

En límites no queremos llegar a "infinitamente grande", sino ir "infinitamente cerca". Cuando escribimos ${\displaystyle \underset{\mathrm{}}{}\mathrm{}}$, queremos decir que siempre podemos estar más y más cerca de $\mathrm{}$.

PROBLEMA 4

¿Cuál es una estimación razonable para ${\displaystyle \underset{\mathrm{}}{}}$?

Escoge 1 respuesta:

Escoge 1 respuesta:

• (Elección A)   

  $\mathrm{}$
• (Elección B)   

  $\mathrm{}$
• (Elección C)   

  $\mathrm{}$
• (Elección D)   

  $\mathrm{}$
• (Elección E)   

  El límite no existe

Otro ejemplo: ${\displaystyle \underset{\mathrm{}}{}{}^{\mathrm{}}}$

Analizemos ${\displaystyle \underset{\mathrm{}}{}{}^{\mathrm{}}}$, que es el límite de la expresión ${}^{\mathrm{}}$ cuando $$ se acerca a $\mathrm{}$.

$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$\mathrm{}$$$$$${}^{\mathrm{}}$

Se grafica la función y = x cuadrada. El eje x va de menos 4 a 6. La gráfica consta de una curva. La curva es una parábola que empieza en (menos 3, 9), se mueve hacia abajo, pasa por (menos 1, 1) y por (0, 0), se mueve hacia arriba, pasa por (1, 1) y termina en (3, 9).

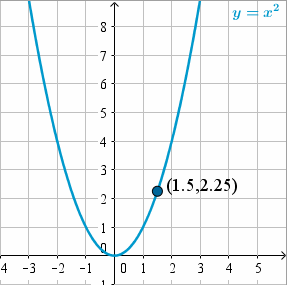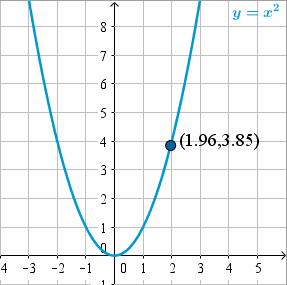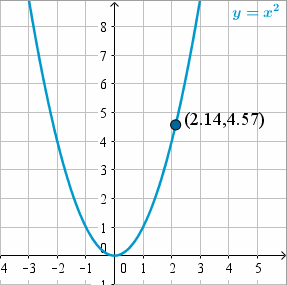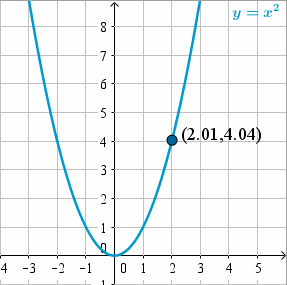
Podemos ver en la gráfica que cuando nos acercamos al punto donde $\mathrm{}$, los valores de $$ están más y más cerca de $\mathrm{}$.

La gráfica de y = x cuadrada está animada con un punto que se mueve hacia arriba sobre la curva desde (1.5, 2.25) hasta (1.99, 3.96) y después se mueve hacia abajo sobre la curva desde (2.5, 6.25) hasta (2.01, 4.04).

Creado con Geogebra.

También podemos observar esta tabla de valores:

También podemos ver cómo nos podemos acercar a $\mathrm{}$ tanto como queramos. Supongamos que queremos estar a menos de $\mathrm{}$ unidades de $\mathrm{}$. ¿Cuál valor de $$ cercano a $\mathrm{}$ podemos escoger?

Intentemos $\mathrm{}$:

${\mathrm{}}^{\mathrm{}}\mathrm{}$

Este valor está a más de $\mathrm{}$ unidades de $\mathrm{}$. Bueno, intentemos $\mathrm{}$:

${\mathrm{}}^{\mathrm{}}\mathrm{}$

¡Este valor ya está suficientemente cerca! Al intentar valores de $$ que están más y más cerca de $\mathrm{}$, podemos acercarnos aún más a $\mathrm{}$.

En conclusión, ${\displaystyle \underset{\mathrm{}}{}{}^{\mathrm{}}\mathrm{}}$.