- Concepto de continuidad
- Continuidad de las funciones elementales
- Límites laterales
1. Concepto de continuidad
Intuitivamente, una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, sin levantar el lápiz del papel.
Ejemplo de función continua: .
Gráfica:
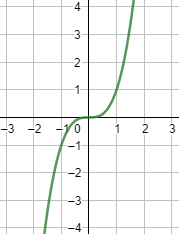
Ejemplo de función no continua: .
Gráfica:
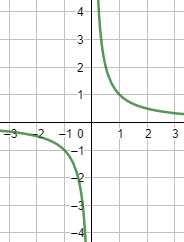
Definición formal:
La función es continua en el punto si
La función es continua si es continua en todos los puntos.
Por ejemplo, la función no es continua en porque no existe .
Observaciones:
En realidad, para hablar de continuidad en un punto , debería ser indispensable que el punto pertenezca al dominio de la función.
Por ejemplo, el dominio de es
y la función es continua en su dominio. Sin embargo, no existe el límite decuando ni existe , por lo que decimos que no es continua en .Como normalmente consideramos a todas las funciones como , tenemos que calcular primero el dominio de la función y, después, la continuidad en el dominio.
2. Funciones elementales
Funciones polinómicas
Son continuas en todos los reales.
Funciones racionales
Son continuas en todos los reales excepto en los que anulan al denominador.
Funciones exponenciales
Como regla general, son continuas en todos los reales. Cuando la base es no positiva, , puede haber complicaciones.
Funciones logarítmicas
Son continuas en todos los reales positivos.
Funciones irracionales
Si es par, son continuas en todos los reales. Si es impar, en los reales positivos.
Funciones trigonométricas
El seno y el coseno son continuas en todos los reales. La tangente no es continua en para todo entero .
La mayoría de las funciones que veremos son combinaciones de las anteriores, así que es recomendable aprender su continuidad.
3. Límites laterales Intuitivamente, el límite de una función
cuando es el valor al que se aproxima cuando se aproxima a .
Sin embargo, en ocasiones, la función se aproxima a uno u otro valor según si se aproxima a por la izquierda o por su derecha. Por esta razón existe el concepto de límite lateral.
Límite lateral de cuando tiende a por la izquierda:
Límite lateral de cuando tiende a por la derecha:
Si los límites laterales no coinciden, diremos que no existe el límite:
Si coinciden, entonces
Por ejemplo, la gráfica de es
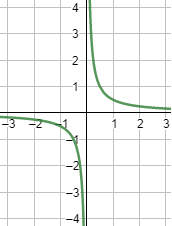
En la gráfica se observa que
- Cuando se aproxima a 0 por la derecha, la función crece indefinidamente:
- Cuando se aproxima a 0 por la izquierda, la función decrece indefinidamente:
Por tanto, no existe el límite cuando :
Intuitivamente, el límite de una función cuando es el valor al que se aproxima cuando se aproxima a .
Sin embargo, en ocasiones, la función se aproxima a uno u otro valor según si se aproxima a por la izquierda o por su derecha. Por esta razón existe el concepto de límite lateral.
Límite lateral de cuando tiende a por la izquierda:
Límite lateral de cuando tiende a por la derecha:
Si los límites laterales no coinciden, diremos que no existe el límite:
Si coinciden, entonces
Por ejemplo, la gráfica de es

En la gráfica se observa que
- Cuando se aproxima a 0 por la derecha, la función crece indefinidamente:
- Cuando se aproxima a 0 por la izquierda, la función decrece indefinidamente:
Por tanto, no existe el límite cuando :
link para descargar null- link para descarga https://youtu.be/UfOvXKxvSMY
Comentarios
Publicar un comentario